Lab 10 report (Grid Localization using Bayes Filter)

In this lab, I use Bayes filter to implement grid localization.

Shihming Lin
Apr 28, 2024

Bayes Filter Overview

Figure 1: Bayes Filter Algorithm (modified from lecture slides)

Implementation of Bayes Filter

Prediction Step

  -   Compute Control

To predict the pose of the robot, I need the the odometry motion model , which needs the relative odometry motion of the robot. The relative odometry motion is in the format (initial rotation 'delta_rot_1', translation 'delta_trans', final rotation 'delta_rot_2') and can be computed from the previous pose(state) and the current pose(state) of the robot.

Figure 2: Relative Odometry Motion (modified from lecture slides)
  -   Odometry Motion Model

Then, the odometry motion model can be built to calculate how likely it is that the robot's state transitions from the previous pose to the current pose under the actual control actions.

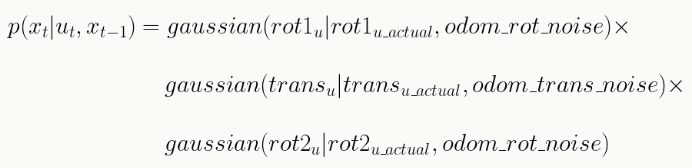
Figure 3: Odometry Motion Model (modified from lab website)
  -   Prediction Step

Finally, the probability of the robot reaching each potential state can be calculated based on its previous state and control inputs. This requires two nested sets of loops, each with three loops iterating over the x, y, and theta dimensions of the previous and current states, respectively. To reduce the computation time, I omits states with a probability lower than 0.0001, as they have negligible impact. After prediction and update, the belief matrix is normalized to ensure that the sum of probabilities across all states equals 1.

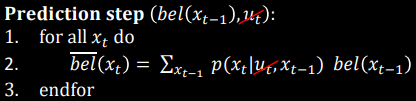
Figure 4: Prediction Step (modified from lecture slides)

Update Step

Sensor Model

The filter next requires a sensor model to update the estimate of the robot state based on the sensor data. The model aims to compute the probability of actual sensor observations and store these probabilities in a one-dimensional array with 18 elements. It utilizes the sensor noise variable and computes each probability using a Gaussian distribution.

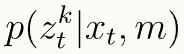
Figure 5: Sensor Model (modified from lab website)

Update Step

The update step for the Bayesian filter is to adjust the belief matrix based on the robot's sensor readings. This involves examining each cell in the grid and calculating the likelihood that the robot is located in that cell based on the sensor data. After calculating the likelihood of each cell, the belief matrix is updated accordingly. Finally, the matrix is normalized to ensure that the total probability of all cells is equal to 1, thus ensuring that it remains a valid probability distribution.

Figure 6: Update Step (modified from lab website)

Demo

Discussion

In the video, the blue line represents "beliefs" which is the most likely state after each iteration of the Bayes Filter, the green line represents "ground truth", and the red line represents "measurements". You can see that the blue line follows the red line in most cases, only when the robot moves a short distance, the updated position will be inaccurate because we only split the map into large grids.

Back to All Reports of Fast Robots Labs